如何进行算法分析？

1.前言
2.数学基础
3.时间复杂度定义
5.实践分析

1.前言

前几天在一篇微信公众号【算法与数据结构】上看到一篇关于算法时间复杂度分析基础的文章，写的比较基础但却不通透。

所以我决定把大学的的老东西翻一翻，整理一篇自我感觉基础通透的知识点。

2.数学基础

我们常常说哪种算法好，说的是对于大量数据计算时算法的相对增长率较小，直白的说就是在最短时间内给出结果。

对于相对增长率，我们由小到大列一些常见的数学函数：

A. 对数函数 logN 【未声明的话，以2为底】

B. 幂函数 N^2、N^3、N^4…

C. 指数函数 2^N

以下是N>0的各函数曲线

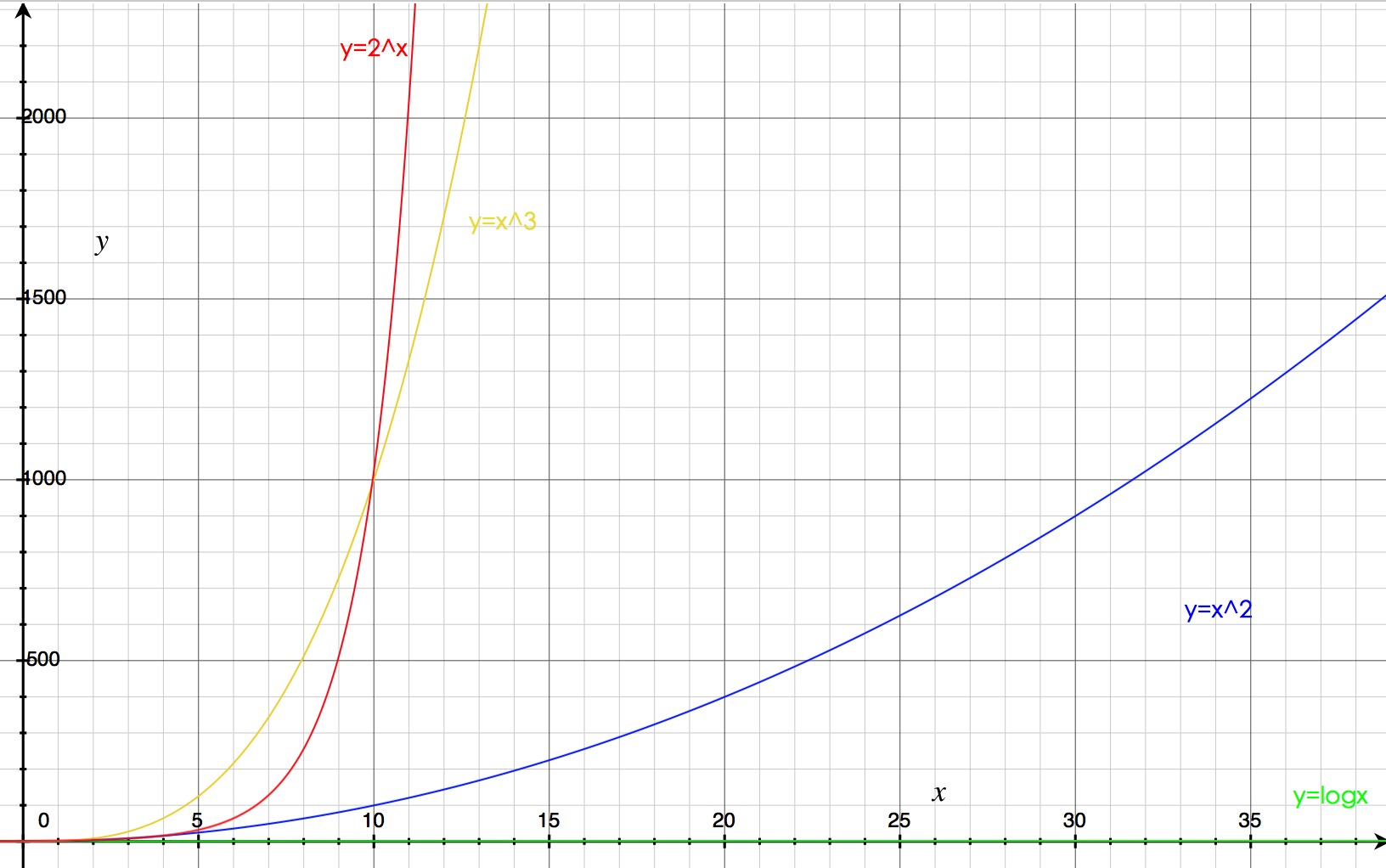
通过对数函数、幂函数、指数函数的曲线图可以看出增长率由小到大今次是：对数函数、幂函数、指数函数。

当然还有其它级别的函数应用于算法当中，这里只做个引导吧。

3.时间复杂度定义

一般我们用T(N)来表示时间复杂度，T(N)的只是表示一个级别，并不是真正的精确表示某个算法的时间复杂度，这个后面我们具体来说，先来说一说T(N)的几个定义。

定义1：如果存在正常数c和n使得当N≥n时T(N)≤cf(N)，则T(N) = O(f(N))【大O标记】;

定义2：如果存在正常数c和n使得当n≥n时T(N)≥cg(N)，则T(N) = Ω(f(N))【omega标记】;

定义3： T(N) = Θ(h(N))【theta标记】当且仅当T(N) = O(h(N))和T(N) = Ω(h(N));

定义4：如果对每一个正常数c都存在常数n使得当N>n时T(N)<cp(N),则T(N)=o(P(N)),或者说如果T(N)=O(p(N))且T(N)≠Θ(p(N)),则T(N)=o(p(N))【小o标记】;

为什么定义以上？主要是为了在函数间建立相对的级别，之前我们提到增长率这个词，在大数据场景我们在分析算法好坏时更多的是分析相对增长率的快慢。

举个粟子：g(N)=100N  h(N)=N^2

对于较小的数时，g(N) > h(N)的，但我们知道h(N)以增长速度更快，简单的说就是斜率

f(N)的斜率 g`(N) = 100

h(N)的斜率 h`(N) = 2N

我们发现 g(N)以稳定的斜率100增长，而h(N)的斜率是随着N的增大而增大的，最终h(N)的斜率终将远远大于g(N)的斜率

对于定义1，拿上面g(N),h(N)的粟子来说，c=1、n=100时g(N)=h(N), 而对于n>100的情况，h(N)总是大于g(N)

对此我们可以用大O标记法来表示： 100N = O(N^2)，即T(N)的增长率小于或等于f(N)

同理：

对于定义2，表示T(N)的增长率大于或者等于g(N)

对于定义3，表示T(N)的增长率等于h(N)的增长率

对于定义4，表示T(N)的增长率小于p(N)的增长率

那么问题来了，对于函数f(N)=4N^2，按照定义1推论f(N)=O(N^4)、f(N)=O(N^3)、f(N)=O(N^2)都是符合的，但显然f(N)=O(N^2)是最严谨的表示。

4.实践分析

Code Demo

public class Demo{

    public static void main(String[] args){

        int sum=0;

        for(int i=0; i<N,i++){

            sum += i*i;
        }

        System.out.println(sum);
    }
}

头尾初始化各占一个时间单元:2

循环初始化i占一个时间单元: 1

判断占N个时间单元: N

i自增占N个时间单元: N

循环内部每次占3个时间单元，N次循环后占：3N

打印输出占一个时间单元：1

总的时间是：5N+4 = O(N)

资料参考：【高等代数】【数据结构与算法分析】

如何进行算法分析？